Geometria Espacial.
1- PIRÂMIDES
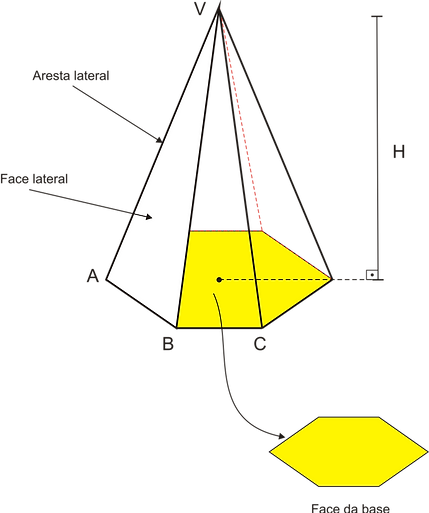
---> Considere um ponto "V" e um polígono em um plano, ligando-se "V" aos vértices do polígono obtem-se um poliedro chamado de pirâmide.


►Toda pirâmide possui:
- n faces laterais
- n+1 faces totais
- n arestas laterais
- 2*n arestas
- Altura = H
(distância entre o vértice e a base)
►ÁREA LATERAL E ÁREA TOTAL:
- Área lateral (SL): é a soma das áreas de todas as faces laterais da pirâmide
- Área total (St) : é a soma da área lateral com a área da base
►O polígono da base é quem dá nome a pirâmide
- Pirâmide triângular ou tetraedro: base feita por um triângulo
- Pirâmide quadrangular: base feita por um quadrilátero
- Pirâmide hexagonal: base feita por um hexágono
- E assim sucessivamente
2- PIRÂMIDE REGULAR
• A base é um polígono regular;
• A altura se encontra com o centro da base;
• Todas as arestas laterais são congruentes;
• As faces laterais são triângulos isóceles.
2.1- AS RELAÇÕES DA PIRÂMIDE REGULAR

3- ÁREA E VOLUME DAS PIRÂMIDES
--> Uma pirâmide possui área lateral(SL) e área da base(SB), sendo a área total a soma das áreas das bases com a área lateral.
►ÁREA LATERAL (SL) E ÁREA TOTAL (ST)
►VOLUME (V)

4- TRONCO DE PIRÂMIDE
--> Seccionando uma pirâmide com um plano paralelo a base criamos dois sólidos: uma pirâmide menor (semelhante a maior) e um tronco de pirâmide.

4.1- EQUIVALÊNCIA ENTRE PIRÂMIDES

4.2- TRONCO DE PIRÂMIDES

►ÁREA LATERAL (SL) E ÁREA TOTAL (ST)
SL = soma da área das faces laterais do tronco da pirâmide.
(obs:num tronco de pirâmide regular as faces laterias são trapézios isóceles)
ST = SL + SB +Sb
SB = área da base maior / Sb = área da base menor
►VOLUME (V)
V = h * (SB + Sb + √SB*Sb )
3

